Закон Кеплера — открытие о взаимодействии планет и Солнца, его формула и глобальное значение для нашего понимания космоса
Закон Кеплера – один из важнейших законов, открытых немецким астрономом Иоганном Кеплером в XVII веке. Закон Кеплера формулирует закономерности движения планет вокруг Солнца и имеет фундаментальное значение для современной астрономии.
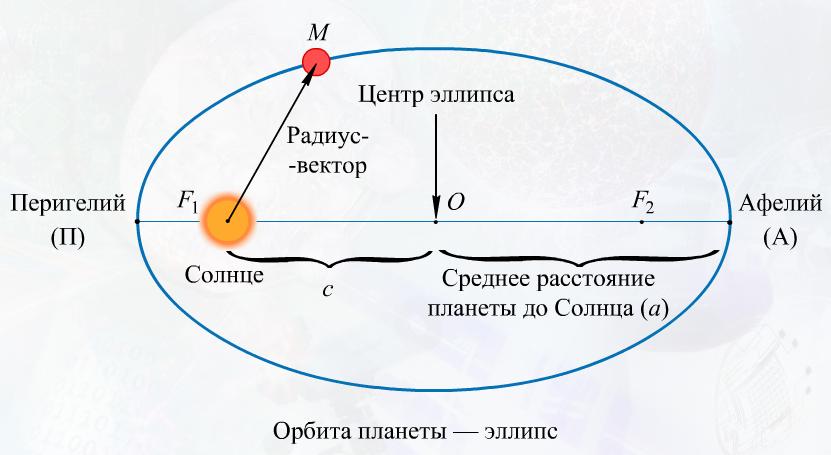
Первый закон Кеплера, известный как закон орбит, гласит, что планеты движутся по эллипсам, где один из фокусов находится в Солнце. Этот закон позволяет точно описать форму орбиты планеты и определить ее радиусы и эксцентриситет. Формула, описывающая орбиту планеты, выражается следующим образом:
r = a * (1 — e * cos(θ))
Где r – радиус вектор, определяющий расстояние между планетой и Солнцем; a – большая полуось орбиты, которая определяет длину самого длинного отрезка эллипса; e – эксцентриситет, характеризующий степень отклонения эллипса от круга; θ – эклиптическая долгота, угол между линией от планеты до Солнца и некоторой начальной линией.
Второй закон Кеплера, закон равных площадей, утверждает, что радиус вектор, проведенный из Солнца к планете, за равные промежутки времени равными площадями пропорционален. Этот закон представляет собой выражение закона сохранения момента импульса и позволяет определить скорость планет при движении вокруг Солнца.
Третий закон Кеплера, закон гармонии, устанавливает связь между периодом обращения планеты вокруг Солнца и ее расстоянием от центрального облегченного тела. Формула этого закона выражается следующим образом:
T^2 = k * a^3
Где T – период обращения планеты вокруг Солнца, a – большая полуось орбиты, k – пропорциональность, зависящая от массы Солнца и планеты. Этот закон позволяет определить период обращения любой планеты вокруг Солнца при известной его радиуса.
Формула закона Кеплера
T^2 = k * r^3
Где:
- T — период обращения планеты вокруг Солнца
- k — гравитационная постоянная, зависящая от Солнца
- r — среднее геометрическое расстояние между Солнцем и планетой
Формула закона Кеплера объясняет, что квадрат периода обращения планеты прямо пропорционален кубу среднего расстояния от планеты до Солнца. Это означает, что при увеличении расстояния между планетой и Солнцем в 2 раза, период обращения планеты увеличивается примерно в 8 раз.
Формула закона Кеплера была открыта немецким астрономом Иоганном Кеплером в начале XVII века. Она сыграла важную роль в развитии астрономии и помогла установить закономерности движения планет в Солнечной системе.
Орбита планеты и Солнца
Первый закон Кеплера гласит, что орбита планеты является эллипсом, и Солнце находится в одном из фокусов этого эллипса. Второй закон Кеплера устанавливает, что планета движется вокруг Солнца с постоянной скоростью, так что радиус-вектор, соединяющий Солнце и планету, за равные интервалы времени описывает одинаковые площади. Третий закон Кеплера определяет зависимость периода обращения планеты вокруг Солнца от большой полуоси орбиты и массы Солнца.
Орбита планеты и ее форма имеют важное значение для понимания ее движения и взаимодействия с другими небесными телами. Закон Кеплера помогает установить закономерности и законы, которые определены природой и позволяют предсказывать движение планет, а также других небесных тел в Солнечной системе.
Период обращения планеты
Закон Кеплера гласит, что квадрат периода обращения планеты прямо пропорционален кубу большой полуоси ее орбиты. Формула для расчета периода обращения планеты имеет вид:
T^2 = k * a^3
Где T — период обращения планеты, a — большая полуось орбиты, k — постоянная, зависящая от массы и гравитационной постоянной Солнца.
Для каждой планеты в Солнечной системе этот период разный. Например, период обращения Земли составляет примерно 365,25 дней.
Интересно отметить, что более удаленные планеты имеют большие периоды обращения. Например, Нептун, которая находится на большом расстоянии от Солнца, имеет период обращения около 165 лет, в то время как Меркурий, самая близкая планета к Солнцу, обращается вокруг него за 88 дней.
Значение закона Кеплера
Первый закон Кеплера, известный также как закон орбит, утверждает, что планеты движутся по эллиптическим орбитам с Солнцем в одном из фокусов. Это означает, что орбиты планет не являются круговыми, как предполагалось ранее, а имеют некоторую степень эксцентричности. Этот закон позволяет объяснить различные физические явления, связанные с движением планет.
Второй закон Кеплера называется законом радиус-вектора и определяет скорость изменения площади, заметаемой радиус-вектором, проведенным от Солнца к планете, за равные промежутки времени. Это означает, что планеты двигаются быстрее на ближайшем к Солнцу участке орбиты и замедляются на более удаленных участках. Закон радиус-вектора помогает объяснить, почему планеты проходят перигелий и афелии с разной скоростью.
Третий закон Кеплера, известный как закон периодов, связывает период обращения планеты вокруг Солнца с средним расстоянием между ними. Он утверждает, что квадраты периодов обращения планет пропорциональны кубам их больших полуосей. Этот закон позволяет определить относительные периоды обращения планет и предсказывать их сопоставительную длительность.
Закон Кеплера имеет огромное значение в научных исследованиях и обеспечивает понимание механизмов движения планет и других тел в космосе. Он является фундаментом для дальнейших открытий и исследований, а также формирует основу для современной астрономической теории.
Подтверждение гелиоцентрической системы
Одним из важных подтверждений гелиоцентрической системы стало открытие Галилео Галилея в начале XVII века. С помощью телескопа он наблюдал фазы Венеры и спутники Юпитера, и эти наблюдения подтвердили идею, что планеты движутся вокруг Солнца.
Другое подтверждение гелиоцентрической системы пришло с открытиями Иоганна Кеплера. Он провел детальные наблюдения планет и сформулировал законы движения планет, которые можно объяснить только в рамках гелиоцентрической системы. Например, его третий закон Кеплера (закон периодов) показывает, что отношение кубов расстояний планет до Солнца квадратам их орбитальных периодов вокруг Солнца является постоянным.
Современные наблюдения космических аппаратов и телескопов также подтверждают гелиоцентрическую систему. Например, измерение расстояний до планет и орбитальных скоростей подтверждают, что они совпадают с предсказаниями, основанными на гелиоцентрической модели.
В целом, гелиоцентрическая система подтверждается как историческими открытиями, так и современными научными наблюдениями. Она является основной моделью Солнечной системы в современной астрономии и космологии.
| Подтверждение | Ученый | Открытие/открытия |
|---|---|---|
| Наблюдения фаз Венеры и спутников Юпитера | Галилео Галилей | Начало XVII века |
| Законы движения планет | Иоганн Кеплер | Середина XVII века |
| Современные наблюдения космических аппаратов и телескопов | — | — |
Планетарные движения
Закон Кеплера — это основа для понимания и описания планетарных движений. Закон Кеплера включает в себя три основных принципа, описывающих движение планет вокруг Солнца. Первый закон Кеплера, или закон орбит, говорит о том, что планеты движутся по эллиптическим орбитам с Солнцем в одном из фокусов.
Второй закон Кеплера, или закон равных площадей, утверждает, что скорость, с которой планета движется вдоль орбиты, такова, что за равные промежутки времени она охватывает равные площади в плоскости орбиты.
Третий закон Кеплера, или закон периодов, гласит, что квадраты периодов обращения планет вокруг Солнца пропорциональны кубам больших полуосей их орбит.
Значение планетарных движений заключается в том, что они позволяют нам понять, как планеты движутся по орбитам и что их движение имеет закономерности. Изучение этих закономерностей позволяет нам предсказывать положение планет в будущем и лучше понять устройство вселенной.
Интерес к планетарным движениям сохраняется и в настоящее время. С помощью современных технологий астрономы могут более точно изучать планеты и их движение, расширяя наше знание о Вселенной.
Вопрос-ответ:
Какая формула закона Кеплера?
Формула закона Кеплера выглядит следующим образом: T^2/R^3 = k, где T — период обращения планеты вокруг Солнца, R — среднее расстояние планеты от Солнца, k — постоянная, которая отличается для разных планет.
Зачем нужен закон Кеплера?
Закон Кеплера описывает движение планет вокруг Солнца и является фундаментальным законом астрономии. Он позволяет определять период обращения планеты, среднее расстояние до Солнца и другие характеристики планетного движения.
Каким образом закон Кеплера был получен?
Закон Кеплера был получен на основе наблюдений и анализа данных о движении планет, сделанных немецким астрономом Иоганном Кеплером в 17 веке. Кеплер провел долгую серию наблюдений Марса и выявил закономерности, которые позволили ему сформулировать эмпирические законы, включающие в себя три закона Кеплера.
Какое значение имеет постоянная k в формуле закона Кеплера?
Значение постоянной k в формуле закона Кеплера зависит от планеты. Для каждой планеты значение k разное. Например, для Земли значение k примерно равно 1. От значения постоянной k зависит период обращения планеты и среднее расстояние от планеты до Солнца.
Можно ли использовать формулу закона Кеплера для других космических объектов?
Формула закона Кеплера, T^2/R^3 = k, применима только для движения планет вокруг Солнца. Для других космических объектов, таких как спутники, астероиды или кометы, необходимо использовать другие формулы или законы.
Какие законы открывает Закон Кеплера?
Закон Кеплера открывает три закона движения планет вокруг Солнца.
Какую формулу использовал Кеплер для описания движения планет?
Кеплер использовал формулу P^2 = a^3, где P — период обращения планеты вокруг Солнца, а a — большая полуось орбиты планеты.